
What is Fractals For SketchBlock?
An advanced fractal generator for SketchBlock, with a wide range of variable parameters, enabling the creation of many, many, different fractal based animations and still images. From tradtional mandlebrot and julia sets, to more complex hybrid images.
Getting Fractals For SketchBlock
You may now purchase and download Fractals For SketchBlock via the AmiStore. Please note if you choose the convenience of AmiStore any updates or bugfixes will be available through the AmiStore system only.
What will I get?
Fractals For SketchBlock consists of the binary fractals.ptf transform plugin for SketchBlock, plus the Fractals.py script which provides an easy to use users interface, and a selection of presets. Advanced users may program the plugin directly via SketchBlock's arexx interface for even greater power.
What do I need?
Fractals for SketchBlock requires the following software to be preinstalled to be useful:
- SketchBlock 2.6 - download If you have SketchBlock Lite, available from AmiStore, then Fractals For SketchBlock version 1.5 and up will adopt the current used SketchBlock theme.
- ProAction 1.7 - download
- PIL (Python Imaging Library) this is used indirectly for export of frames via the ExportAs.py SketchBlock script. - download
- AISS 4.12 (for toolbar images) - download
Now I've Got It How Do I Install It
Fractals For SketchBlock comes with a standard instaler script. So unpack the archive (RAM: is a good place) and double click on the installer, this will locate your SketchBlock install and copy the files to the correct place. It will also offer the option to add Fractals to the Misc menu in SketchBlock.
Amiga user Epsilon wrote a very nice blog about installing Fractals For SketchBlock and makes the process clearer than I ever could. Read it here.
Once installed you can start Fractals For SketchBlock by double clicking on it's icon, (this must be done after starting SketchBlock) or if you chose the menu option, by invoking the Misc->Fractals menu from within SketchBlock.
A Little Bit Of Maths
If you find maths scary you an skip this bit, but here is a short description of the mathematics used by Fractals, understanding it will help you understand the many options in the program interface, on the other hand understanding it is not neccessary at all.
In the following "z" is a complex number of the form

and so can be used to represent a point in the plain of the image.
Fractals are calculated by iterating a function for each point in the plane so that:

and checking whether the magnitude of z diverges / converges or remains the same. The points that remain the same are technically the ones that are part of the "set". In practice we test how many interations the magnitude of the z value stays below 2 as it can be proved that once above 2 it always diverges.
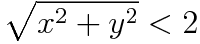
or more efficiently
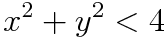
Fractals For SketchBlock (FFSB from now on) uses the following main equation

where
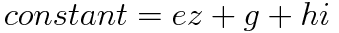
The constant term is only calculated for the first iteration thus the term in ez is different to the earlier cz and has quite a different effect on the outcome.
Expanding the terms in Z and gathering the real and imaginary parts togther we get:
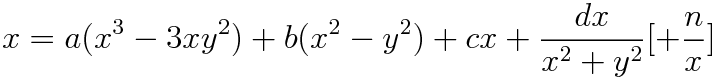
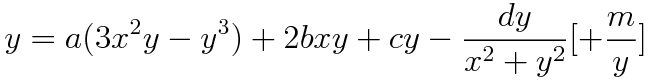
Notice the terms in square brackets at the end of each equation, these extra option terms do not come from main iteraction equation but were added experimentally as they create quite an interesting swirled effect in the fractal images.
By varying the values of the variable "a", "b", "c" etc etc we produce a wide range of different fractals. For example
- b = 1.0 and e = 1.0 gives:
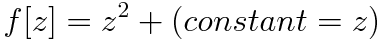
The equation for the Mandelbrot set. - b = 1.0 and g = 0.4 h = 0.4 gives:
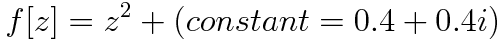
A julia set.
How Do I use it?
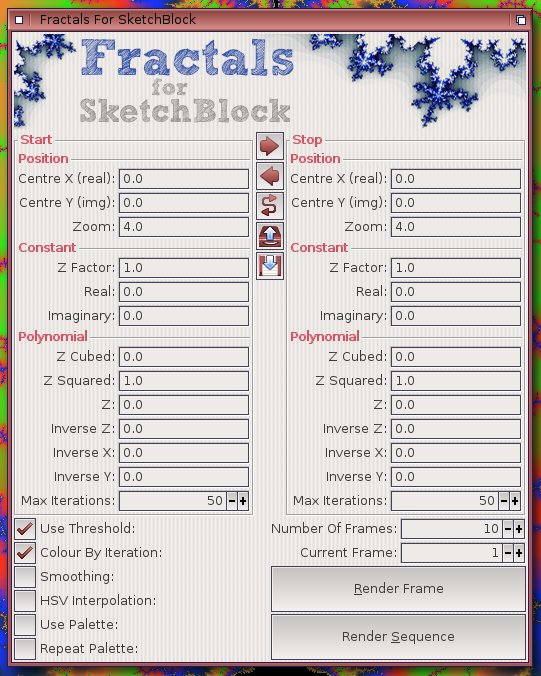 As you can see from the screenshot to the right of the page, the FFSB gui is divided into two symtrical sections, with
the left half defining the 'start' setup and the right defining the 'stop' setup. The gadgets at the bottom of the window define some global behaviours, how many frames, which still frame to render etc etc.
As you can see from the screenshot to the right of the page, the FFSB gui is divided into two symtrical sections, with
the left half defining the 'start' setup and the right defining the 'stop' setup. The gadgets at the bottom of the window define some global behaviours, how many frames, which still frame to render etc etc.
Defining The Fractal
Position
This section allows you to position and scale the fractal image on the plane. The coordinates are in terms of the complex plane, not the absolute pixel values, they vary from -2.0 to + 2.0 in the real (x) and imaginary (y) axis. At first thought this would be hard to work out, but here's a tip, just click on the SketchWindow and the 'start' coordinates will be entered for you, shift click for the 'stop'.
The zoom gadget defines how much of the complex plane is shown in the image, smaller is bigger in this regard! You can zoom out to 4.0 and in to 0.000001 a range of 4 Million!
Constant
This section sets up the constant term as described in the maths section above. More z makes a more mandlebrot style fractal, more real and imaginary make for a more julia set style, and endless points in between. Values vary from -2.0 to 2.0 (anything larger automatically diverges and so leaves you with a plain white page ). Experiment with different values to find the sweet spots with the most interesting results.
Polynomial
Here we define the factors determining how the different terms in the main equation above are combined. Values vary from -2.0 to 2.0, though you find with the inverse factors, smaler values (0.1 -> 0.5 for Z and as low as 0.01 for X & Y) work better.
Max Iterations
This is the point at which we stop testing for divergence, if the equation hasn't diverged by this time we assume that it never will and mark the point part of the set. The higher this value, the more details, but there is limit to how much detail may be displayed at any resolution, more iterations are need at higher zooms.
Global Options
Use Threshold
With this set we stop iterating as soon as the magnitude of Z excedes 2.0, otherwise we cary on calculating to find the end value after the Max Iterations have been reached.
Colour By Iteration
With this set we colour the pixel according to the number of iterations required to excede the threshold of 2.0, naturally this can only work when Use Threshold is active. Otherwise we use the final calculated value to determine the colour.
Smoothing
Switches on smoothing for iteration based colouring. The algorithm works best for small colour steps, so for best smooth effects use palettes with a gradual colour sequence.
HSV Interpolation
Use HSV colour space for interpolating colours when smoothing or when interpolating between colours in the simple "two colour mode" or norepeating palette mode.
Use Palette
As well as the background and foreground colours, intermediate stages may be defined by the current pallette, interpolation is used between each palette step, there may be as many colours in the palette as you desire. For smootheset results start and finish the palette with the forground and background colour.
Repeat Palette
With this enabled each palette colour is applied in sequence, one per iteration step, and the palette is repeated as many times as required. Shorter palettes can look very stripey and abit noisey at higher iterations / deeper zooms, so try to use longer evenly spread palettes for best effects.
Number Of Frames
The total number of frames rendered in a sequence. The fractal values will be interplated between the start and stop fractal settings, depending on frame number.
Current Frame
The current single frame to render in the sequence, or if the sequence is being rendered, the frame that was just rendered.
Render Frame
Render a single frame and disply it in the active layer of the active sketchblock project.
Render Sequence
Render as sequence of frames. A file requester will popup to determine the destination directory (default RAM:). Frames will exported as PNGs and be named frame_####.png where #### is the frame number.
 Copy To Stop
Copy To Stop
Copy the current start settings to the stop setup.
 Copy To Start
Copy To Start
Copy the current stop settings to the start setup.
 Swap Settings
Swap Settings
Swap the start and stop settings.
 Load Preset
Load Preset
Load a presaved preset, this might modyfy some or all settings.
 Save Preset
Save Preset
Save the current state to disk.
Low Level Control
The low power is provided by the "Fractal" pixel transform, and can be access by ARexx or python programs via the SketchBlock TransformLayer command.
Here is an overview of the arguments. All 16 arguments must be supplied. Floating point values are premultiplied by 256.0 to increase the "resolution".
- FLOAT - Real (x) Coordinate of centre.
- FLOAT - Imaginary (y) Coordinate of centre.
- FLOAT - Zoom, range of complex plabe dislayed, smaller number = deeper zoom<.li>
- FLOAT - Z Factor of constant term
- FLOAT - Real part of constant term
- FLOAT - Imaginary part of constant term
- FLOAT - Z Cubed factor
- FLOAT - Z Squared factor
- FLOAT - Z factor
- FLOAT - Inverse Z factor
- FLOAT - Inverse X factor
- FLOAT - Inverse Y factor
- ULONG - Maximum number of iterations.
- ULONG - (BOOL)Use threshold for full iterations
- ULONG - (FLAGS) Colouring Options: Or the following values togther
- 1 COLOUR BY ITERATION
- 2 COLOUR SMOOTHING
- 4 COLOUR BY PALETTE
- 8 PALETTE REPEAT
- 16 HSV INTERPOLATION
- ULONG - PaletteID - ID of palette to use or 0xFFFFFFFF (-1) - Use active Palette




